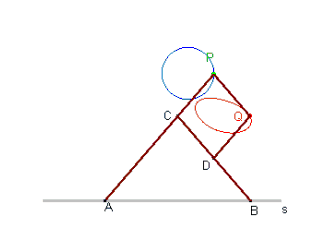
La mostra di macchine matematiche che abbiamo visitato il 9 gennaio con l'accompagnamento e le spiegazioni del professore Buzzanca raccoglie strumenti per la costruzione di curve, la realizzazione di trasformazioni geometriche, la verifica pratica di teoremi. Tra le macchine ho scelto quella che sfrutta il metodo del Delaunay. Per il tracciamento delle curve esistono vari sistemi articolati e strumenti: il matematico Kempe dimostrò infatti che è possibile costruire un sistema articolato per disegnare una qualsiasi curva algebrica nell’intorno di un suo punto (1876). Il metodo del Delaunay si articola così: CPQD è un rombo articolato di lato a. Le aste PC e CD sono prolungate in modo tale che CA=CB=b. Gli estremi A e B sono scorrevoli lungo la guida rettilinea s. I punti P e Q sono corrispondenti in una trasformazione non lineare e quando P percorre una circonferenza, Q descrive la curva ad essa corrispondente (quartica). per una simulazione vi rimando al sito della mostra, che offre interessanti simulazioni sul funzionamento delle macchine:
http://www.museo.unimo.it/theatrum/macchine/_00lab.htm